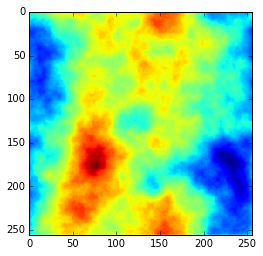
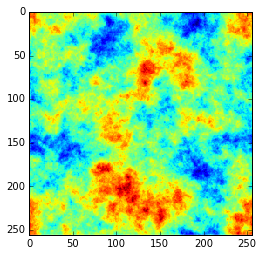
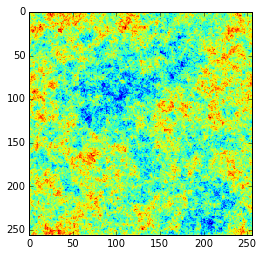
Random fields are an example of a more formally defined noise process that can appear visually similar to some forms of procedurally generated noise like Perlin noise or simplex noise.

There are some really nice of examples of descriptions for random fields and in particular Gaussian random fields on Wikipedia. However, with a few exceptions, there doesn’t seem to be a great deal of literature available on how to generate such fields. Furthermore, while there is the RandomFields package on CRAN for R, there don’t appear to be any well known Python packages.

In the search for a good library, I did find an amazing question on the Mathematica Stack Exchange, where a number of different techniques for genering these fields have been presented.

This Python snippet is a simplified version of the current top voted answer

def fftIndgen(n):
    a = range(0, n/2+1)
    b = range(1, n/2)
    b.reverse()
    b = [-i for i in b]
    return a + b

def gaussian_random_field(Pk = lambda k : k**-3.0, size = 100):
    def Pk2(kx, ky):
        if kx == 0 and ky == 0:
            return 0.0
        return np.sqrt(Pk(np.sqrt(kx**2 + ky**2)))
    noise = np.fft.fft2(np.random.normal(size = (size, size)))
    amplitude = np.zeros((size,size))
    for i, kx in enumerate(fftIndgen(size)):
        for j, ky in enumerate(fftIndgen(size)):            
            amplitude[i, j] = Pk2(kx, ky)
    return np.fft.ifft2(noise * amplitude)

for alpha in [-4.0, -3.0, -2.0]:
    out = gaussian_random_field(Pk = lambda k: k**alpha, size=256)
    plt.figure()
    plt.imshow(out.real, interpolation='none')

Which produces figures like: